January 11, 2026 by Sam Jarman, Phys.org
Collected at: https://phys.org/news/2026-01-physicists-resilient-3d-solitons-lab.html
For the first time, physicists in Italy have created a ‘lump soliton’: an extremely stable packet of light waves which can travel through 3D space, and even interact with other solitons without losing its shape.
Led by Ludovica Dieli at Sapienza University of Rome, the team achieved their result using a specially engineered crystal, whose responses to incoming light beams could be tightly controlled using an external voltage. Their study appears in Physical Review Letters.
Understanding solitons and integrability
A soliton is a short burst of localized waves, which can in theory maintain its shape indefinitely as it propagates, even as it interacts with other waves. This behavior is only possible through a mathematical concept named ‘integrability’: found in nonlinear equations with large numbers of conserved quantities, like energy and momentum. These properties remain constant as the system evolves, making it far more resilient against effects like distortion and turbulence, which can destroy the information carried by the wave.
While truly integrable solitons have been produced in the lab, they have only existed in one dimension—propagating along a single straight line. Yet in 1970, a pair of Soviet physicists introduced a new model, which showed how solitons could realistically propagate through 3D space. Named a ‘lump soliton,’ this wave packet is described by the Kadomtsev-Petviashvili (KP) equation, and its experimental possibility has been actively explored ever since the pair first drew out their theory.
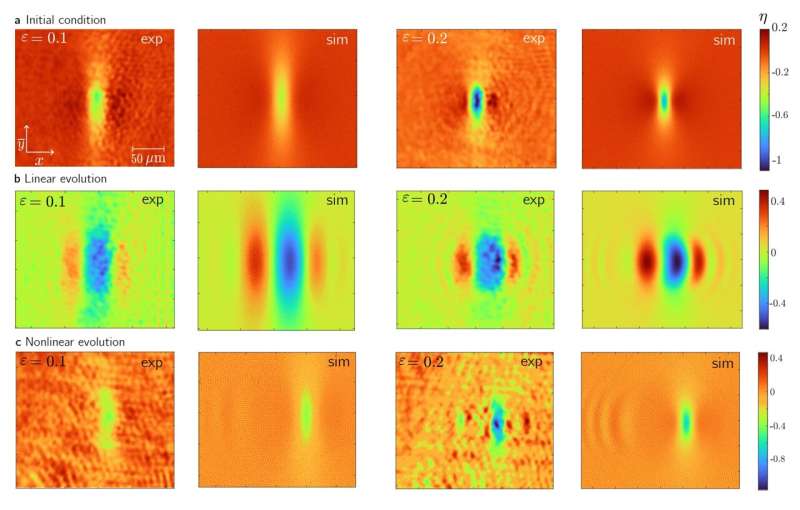
“However, research on the lump soliton continues to lack experimental observation due to the restrictive conditions required by the KP equations to apply to a real physical system,” Dieli explains. “Although nonlinear waves have been extensively studied in recent decades, the study of lump solitons has remained theoretical.”
Experimental breakthrough and implications
In their study, Dieli’s team addressed this challenge using a strontium-barium niobate crystal, whose photorefractive properties cause light to propagate in a controlled, intensity-dependent way. By applying an external voltage to the crystal, the team could generate a 2D ‘photon fluid’: an optical field which flows much like a regular fluid in response to the voltage.
This in turn enabled them to control its ‘nonlinear’ response to an incoming light beam—describing the interrelated changes to beam and fluid as they interact.
“Our setup also allowed us to control the amplitude and phase of the light beam with micrometric accuracy,” Dieli adds. “This tool is essential for preparing the lump soliton’s initial condition, with high fidelity to its analytical form.”
With this carefully controlled approach, the researchers could finally produce the multi-dimensional, truly integrable solitons that had eluded physicists for decades.
“We observed a lump soliton that preserves its analytical shape during propagation, and undergoes a characteristic shift in the 2D plane perpendicular to its motion,” Dieli continues. This shape remained unchanged even as the wave packet collided with an identical lump soliton traveling in the opposite direction: a clear demonstration of its integrability.
The team now hope that their successful experimental result could have promising implications for the future exploration of lump solitons, and nonlinear waves as a whole.
“Our findings pave the way for the experimental investigation of the KPI equation and its solutions, ensuring high fidelity to its analytical form,” Dieli says. “This level of fidelity has never before been achieved in multidimensional nonlinear wave experiments.”
More information: Ludovica Dieli et al, Observation of lump solitons, Physical Review Letters (2025). DOI: 10.1103/ggbs-y21w
Journal information: Physical Review Letters

Leave a Reply