How does deep learning actually work?

October 2, 2025 by Rakesh Kumar, PhD

Collected at: https://www.eeworldonline.com/how-does-deep-learning-actually-work/

Deep learning has added a new dimension to engineering applications, from 5G signal processing to predictive maintenance in power grids. It automatically detects equipment failures and optimizes network traffic with accuracy. But how do these artificial systems actually learn from data?

This FAQ explores the fundamental architecture of neural networks, the two-phase learning process that optimizes millions of parameters, and specialized architectures like convolutional neural networks (CNNs) and recurrent neural networks (RNNs) that handle different data types.

What are the fundamental building blocks of deep learning?

The bedrock of deep learning is the artificial neural network, a computational architecture that processes information through interconnected processing units called neurons. It is a complex signal processing system where each connection represents a programmable gain element.

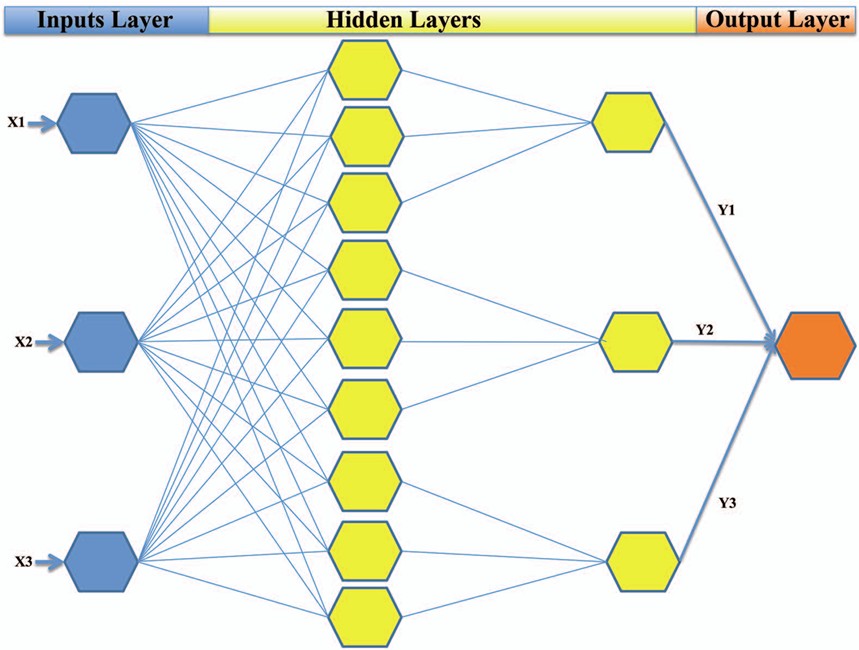
As shown in Figure 1, a deep neural network consists of three fundamental layers: an input layer that receives raw data (such as sensor readings or signal samples), multiple hidden layers that perform increasingly complex feature extraction, and an output layer that produces the final decision or prediction. Each connection between neurons has an associated weight, a numerical parameter that determines the strength of that connection.

“Deep” in deep learning refers to multiple hidden layers, each designed to identify progressively more sophisticated patterns. For instance, in a system analyzing power grid data, the first hidden layer might detect basic voltage fluctuations, the second layer could identify frequency anomalies, and deeper layers might recognize complex fault signatures that indicate equipment degradation.

Each neuron performs a weighted summation of its inputs, followed by a nonlinear activation function. This mathematical operation can be expressed as:

y = f(Σ(wi × xi) + b)

Where wi represents the weights, xi the inputs, b the bias term, and f the activation function. This formulation will be familiar to engineers as a form of linear combination followed by nonlinear processing, similar to operational amplifier circuits with nonlinear elements.

How do neural networks actually learn from data?

Deep learning is very powerful because it has very complex, multi-layered, and often specialized architectures. It can also automatically optimize millions of parameters through a two-phase learning process that works like feedback control systems.

The learning process, illustrated in Figure 2, operates through two distinct phases. Forward propagation resembles signal flow analysis, where input data flows through the network, with each layer applying mathematical transformations to generate increasingly refined representations. The network’s prediction emerges from the output layer after this cascaded processing.

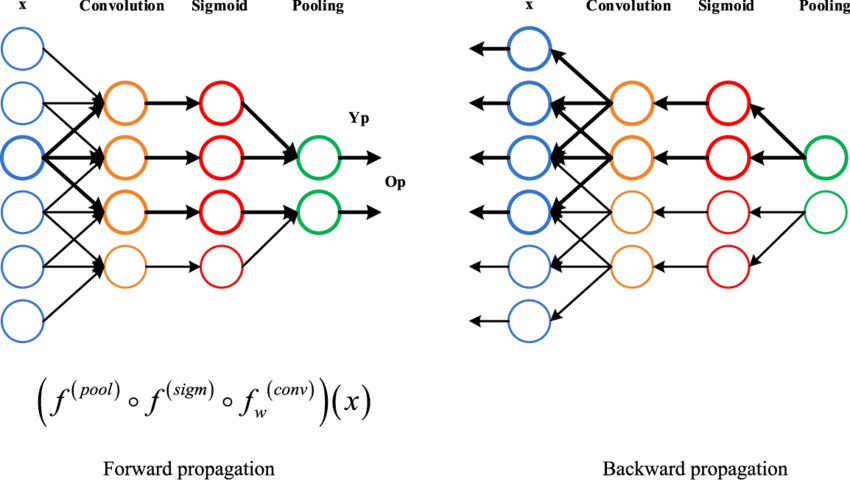
The second phase, backward propagation, implements the learning mechanism. When the network’s prediction differs from the expected result, an error signal is calculated and propagated backward through the network. This process computes the gradient of the error with respect to each weight, determining how each parameter contributed to the overall mistake.

The optimization algorithm, typically gradient descent, then adjusts the weights in the direction that minimizes the error. This iterative process repeats for thousands or millions of training examples, gradually improving the network’s performance. The mathematical elegance lies in the chain rule of calculus, which enables efficient gradient computation through the entire network depth.

For engineers, this process parallels adaptive filter design, where coefficients are continuously updated based on error feedback. However, deep learning extends this concept to nonlinear, multidimensional optimization spaces with higher effectiveness.

Case study: convolutional neural networks for image-based systems

While the fundamental learning principles remain constant, different types of data require specialized network architectures that have proven effective across various domains.

CNNs represent a specialized architecture designed for spatial data processing, as shown in Figure 3. Raw input data goes through a series of operations, alternating between convolution and pooling, which pull out more and more complex features until it is finally classified.

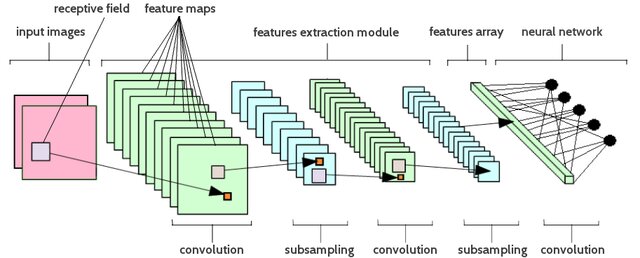
When you use learned filters on the input, the convolution operation looks for certain patterns or features in a planned way. For engineers, this process is similar to digital signal processing. The convolution operations work like adaptive filters that learn the best kernels during training instead of using filter coefficients that have already been set.

The hierarchical processing structure makes a natural feature extraction pipeline: the first layers find simple patterns like edges and textures, and the later layers put these together to make more complex representations. This automated feature learning gets rid of the need for manual feature engineering, which is a significant improvement over older pattern recognition methods.

CNNs can be used to analyze spatial data in a variety of fields, from computer vision to any other area where data can be stored in a grid-like format. For example, in signal processing, time-frequency representations are analyzed as images.

Recurrent neural networks for sequential data analysis

The problem of sequential data analysis is solved by RNNs, which use memory mechanisms and feedback connections to do so. RNNs, unlike feedforward networks, can handle sequences of different lengths and remember what they were fed before.

Figure 4 displays a real-world example of how RNNs work in optical communications. It shows how they handle three types of sequential data: digital signal waveforms, network traffic patterns, and equipment state parameters. The architecture of the network has memory cells that keep data across time steps, which lets you look at how events depend on each other over time.

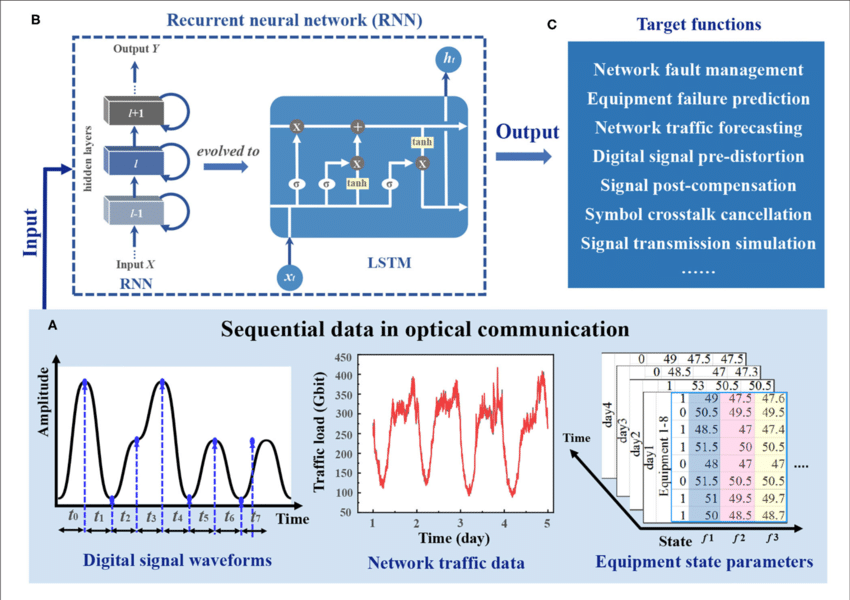
The ability of basic RNNs to learn long-term dependencies is a major limitation that is addressed by the long short-term memory (LSTM) variant. LSTMs use complex gating mechanisms to manage the flow of information, remembering only the important details and forgetting the less important ones.

The applications shown, network fault management, equipment failure prediction, and various signal processing tasks, demonstrate RNN capabilities in communications engineering. Similar principles apply wherever sequential patterns need to be learned from time-series data, though implementation details vary significantly across different engineering domains.

Summary

Neural networks process information through layers connected by weighted connections. They learn through a two-phase cycle in which forward propagation makes predictions and backward propagation finds the best settings. Two types of architectures, convolutional networks for spatial data and recurrent networks for sequential data, show how simple mathematical operations can be used on a large scale to produce complex behaviors.

This automated pattern discovery feature greatly benefits engineering applications like 5G network optimization and predictive maintenance systems. For engineers, deep learning is a powerful computer tool that takes traditional optimization ideas to a level of increased complexity.

References

Deep learning for computer vision: a comparison between convolutional neural networks and hierarchical temporal memories on object recognition tasks, ResearchGate
Artificial Intelligence in Optical Communications: From Machine Learning to Deep Learning, Frontiers in Communications and Networks
Artificial Neural Network in Drug Delivery and Pharmaceutical Research, The Open Bioinformatics Journal
Fault State Recognition of Rolling Bearing Based Fully Convolutional Network, ResearchGate