What are the mathematics of hypersonic flight?

February 7, 2025 by Jeff Shepard

Collected at: https://www.eeworldonline.com/what-is-the-mathematics-of-hypersonic-flight/

The mathematics of hypersonic flight primarily involves fluid dynamics, thermodynamics, and gas dynamics. It particularly focuses on the Navier-Stokes equations, which model the highly compressible airflow and other effects around the missile. It’s all about Mach.

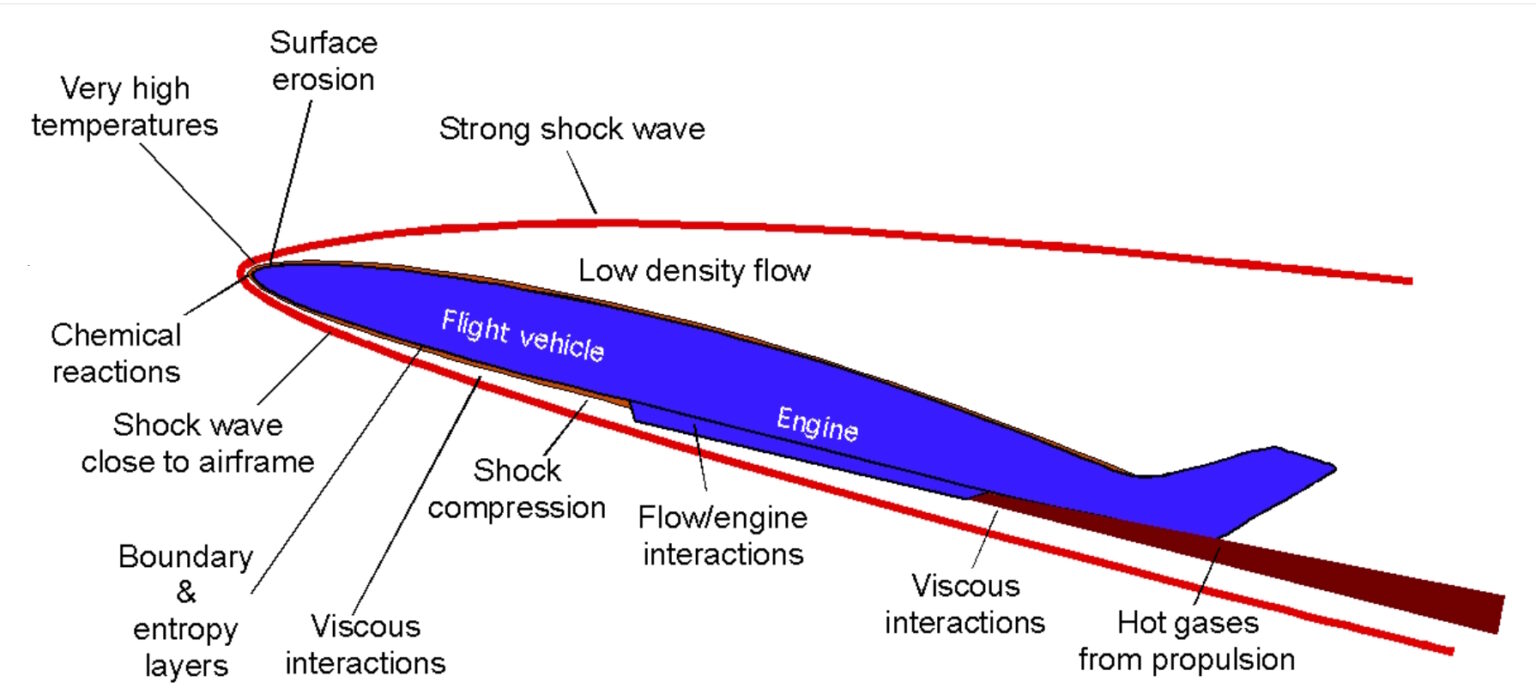
Hypersonic Mach numbers result in numerous aerodynamic design challenges compared to slower speeds. They include the proximity of the shock waves to the surface of the vehicle, related chemical and thermal effects, and how the propulsion system is integrated into the airframe (Figure 1):

• The angle of the shock wave (the Mach angle) relative to the missile is small at high Mach numbers, bringing the sock wave close to the skin. The sine of the Mach angle is directly related to the inverse of the Mach number. The shock wave can interact with the airframe and disrupt boundary airflow.
• The shock wave is also stronger at Mach 5+. That adds to the complications, including chemical interactions and associated surface erosion at the nose of the missile. It also results in extreme heating that requires specialized materials for the skin and control surfaces.
• The propulsion system and airframe must be tightly integrated so the air is pre-compressed by flowing past the skin before entering the engine. That’s essential to support high Mach flights.

Knudsen number and Navier-Stokes equation

The Knudsen number (K_n) is the ratio between the mean free path of molecules in a gas and the characteristic length scale of the system. It’s dimensionless and expressed as K_n = λ / L, where λ is the mean free path, and L is the characteristic length.

K_n indicates how often gas molecules collide compared with the walls of a container (or the skin of a hypersonic missile). It’s used to classify flow regimes of a gas. Interpretation of K_n extremes includes:

K_n << 1 indicates a continuum flow where the gas behaves like a continuous fluid, and the Navier-Stokes equations apply. This is the hypersonic regime.

K_n >> 1 indicates a rarefied flow where the gas molecules are more likely to collide with the walls than each other, requiring specialized kinetic theory approaches.

The Navier-Stokes equations exhibit an extended K_n validity of about an order of magnitude over the Euler equations and can be used to model hypersonic flight (Figure 2). The equations account for the conservation of mass, momentum, and energy. When used to describe hypersonic flight, terms are added to model chemical reactions, thermal considerations, and other factors.

Navier-Stokes in action

The basic Navier-Stokes equations can account for the highly compressed airflow and significant pressures experienced during hypersonic flight. One of the keys to the usefulness of the Navier-Stokes equations is their ability to be modified to account for the unique conditions of hypersonic flight, such as:

• The equations can include terms that model the dissociation and ionization of air molecules resulting from the high temperatures next to the skin of a hypersonic missile and the resulting deviations from ideal gas behavior.
• Additional terms are added to model the concentrations of specific chemical species and the related chemical reactions that can have significant consequences.
• While airflow is primarily inviscid at hypersonic speeds, more terms can be used to model the viscus effects adjacent to the skin. These terms account for shear stresses and heat transfer.

Computational fluid dynamics is generally used to solve hypersonic flows’ complex physics and chemical interactions. Shock waves, turbulence, boundary layers, and heat transfer must be given special consideration.

Accurate and detailed meshing is a prerequisite for capturing complex flow dynamics, especially at the missile’s nose and near sharp edges. The results must be verified with detailed wind tunnel experiments or, even better, by flying prototype missiles.

Summary

The mathematics of hypersonic flight is complex and is all about the Mach number. While the Navier-Stokes equations provide a firm foundation for analyzing hypersonic dynamics, they need to be modified with terms that describe the dissociation and ionization of air molecules, the concentration of specific chemical species, and the interactions between the viscous and inviscid flow regimes around the missile, and other effects unique to traveling at Mach 5+.